Special Relativity

Albert Einstein's 1905 theory of special relativity is one of the most important papers ever published in the field of physics. Special relativity is an explanation of how speed affects mass, time and space. Special relativity applies to "special" cases — when discussing huge energies, ultra-fast speeds and astronomical distances, all without the complications of gravity. Albert Einstein generalized this theory 10 years later in the paper "General Relativity".

Special relativity has a wide range of consequences that have been experimentally verified. They include the relativity of simultaneity, length contraction, time dilation, the relativistic Doppler effect, mass–energy equivalence, the speed of causality, etc.

Reference Frames

Reference frames play a crucial role in relativity theory. The term reference frame as used here is an observational perspective in space that is not undergoing any change in motion (acceleration), from which a position can be measured along 3 spatial axes (so, at rest or constant velocity). In addition, a reference frame has the ability to determine measurements of the time of events using a "clock" (any reference device with uniform periodicity).

Lorentz Factor

To derive the equations of special relativity, one must start with two postulates

The laws of physics are invariant under transformations between inertial frames. In other words, the laws of physics will be the same whether you are testing them in a frame 'at rest', or a frame moving with a constant velocity relative to the 'rest' frame.
The speed of light in a perfect classical vacuum ($c_0$) is measured to be the same by all observers in inertial frames and is, moreover, finite but nonzero. This speed acts as a supremum for the speed of local transmission of information in the universe.

The reason 'rest' is enclosed with quotes is because there is no true rest frame - we will never be able to know whether we are truly at rest or simply travelling at constant velocity. This is all because everything is relative.

The Lorentz factor is used very often in special relativity as it relates the change in time and space at relativistic velocities.

$$ \gamma = \frac{1}{\sqrt{1 - \beta^2}} $$

where $\beta = v/c$ and $v$ is the relative velocity between two inertial frames. For two frames at rest, $\gamma = 1$ and increases with relative velocity between the two inertial frames. As the relative velocity approaches the speed of light, $\gamma \rightarrow \infty$.

Time Dilation

Applying the above postulates, consider the inside of a train moving with a velocity $v$ close to the speed of light with respect to someone standing on the ground as the vehicle passes. Inside, a light is shone upwards to a mirror on the ceiling, where the light reflects back down. If the height of the mirror is $h$, and the speed of light $c$, then the time it takes for light to go up and back down is $t = 2h/c$.

However, to the observer on the ground, the situation is very different. Since the train is moving by the observer on the ground, the light beam appears to move diagonally instead of straight up and down. This path will form two right-sided triangles, with the height as one of the sides, and the two straight parts of the path being the respective hypotenuses. Applying Pythagorean theorem and denoting $t'$ as the time taken for the light to go up and down as viewed by the observer

$$ v^2 {\left( \frac{t'}{2} \right)}^2 + h^2 = {c^2 \left( \frac{t'}{2} \right)}^2 $$

Rearranging to get $t'$

$$ h^2 = \left( c^2 - v^2 \right) {\left( \frac{t'}{2} \right)}^2 $$

$$ {\left( \frac{t'}{2} \right)}^2 = \frac{h^2}{c^2 - v^2} $$

$$ t' = \frac{2h}{\sqrt{c^2 - v^2}} $$

We know that $t = 2h/c$ so $2h = tc$, substituting

$$ t' = \frac{tc}{\sqrt{c^2 - v^2}} $$

$$ t' = \frac{tc}{\sqrt{c^2} \cdot \sqrt{1 - \frac{v^2}{c^2}}} $$

$$ t' = \frac{t}{\sqrt{1 - \frac{v^2}{c^2}}} = \gamma t $$

From this, we obtained the formula for time dilation $t' = \gamma t$. In this example, the time measured in the frame of the train, $t$, is known as the proper time. The proper time between 2 events - such as the event of light being emitted and received on the train - is the time between the two events in a frame where the events occur at the same location. In our case, the emission and reception of light both took place in the vehicle's frame, making the time that an observer would measure in the vehicle's frame the proper time.

Now, let's apply this formula to uncover some interesting phenomena.

Example 1

Because this is physics, let's assume a 15-year-old Alice decides to leave Earth at $99.9\%$ the speed of light and return 5 years later. Alice would have aged by 5 years, but only relative to other people living on Earth, who would have aged much more. This is because Alice was traveling at extremely high speeds, causing the Lorentz factor to be large. $\gamma > 1$. Let's apply the formula to see how much the people would have aged on Earth

$$ t' = \frac{5\;\text{years}}{\sqrt{1 - 0.999^2}} \approx \frac{5}{0.04471} \approx 112\;\text{years} $$

Wow, that's a lot of time; she probably would not be able to see her friends anymore.

Example 2

Now, let's look at a real example in our universe, and a real study. Quoting from the abstract: "Muons are 2nd generation leptons which have a mass of $105 MeV$, $200$ times more massive than an electron, with a negative charge. When cosmic rays hit earth’s atmosphere, pions are created and decay into muons within $26$ nanoseconds. Muons interact electromagnetically with other particles and therefore can travel a relatively long distance while losing energy in the process. The average lifetime of muons is about $2.197$ microseconds and sometimes travel at near the speed of light. According to Classical Mechanics, muons traveling at nearly the speed of will take approximately $50$ microseconds to reach sea level which is $25$ times longer than muon lifetimes. Muons can, however, be detected at sea level at a rate far greater than classical predictions. This is due to time dilation."

Muons travel at roughly $99\%$ the speed of light, and we calculate the Lorentz factor to be roughly $\gamma \approx 7.09$. Thus the average relativistic lifetime of muons is $2.197\mu s \times 7.09 \approx 15.6\mu s$, which is a huge increase from before.

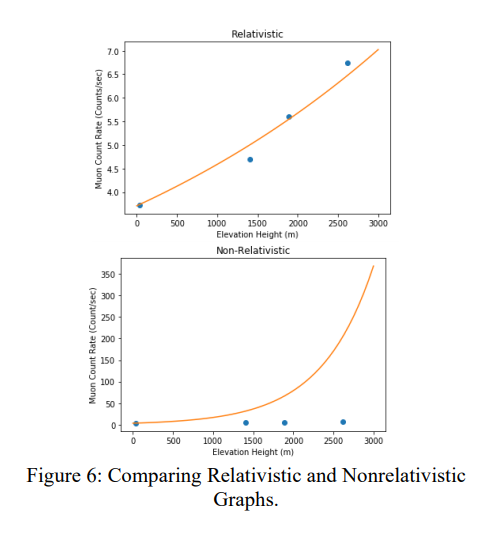
Results

In this figure, the orange line represents the expected muon count rate depending on the existence of time dilation. The blue dots represent actual experimental results, and it is clear that they fit the top graph better. This is just one of many interesting phenomena caused by time dilation.

Length Contraction

Consider a long train, moving with velocity $v$ with respect to the ground, and one observer on the train and one on the ground, standing next to a post. The observer on the train sees the front of the train pass the post, and then, some time $t'$ later, sees the end of the train pass the same post. He would then calculate the train's length as follows: $l = vt'$.

However, the observer on the ground, making the measurement, comes to a different conclusion. This observer finds that time $t$ passed between the front of the train passing the post, and the back of the train by the post. Because the two events occurred in the same place in the ground observer's frame, the time this observer measured is the proper time. Hence

$$ l' = vt = v \left( \frac{t'}{\gamma} \right) = \frac{l}{\gamma} $$

This is the formula for length contraction. Note that length contraction only occurs in the direction of motion, and contraction approaches infinity as $v \rightarrow c$.